Основанием пирамиды служит прямоугольник. Из боковых граней две перпендикулярны к плоскости основания, а две другие образуют с ней углы α и β. Высота пирамиды равна H. Определить объем пирамиды.

Если грани ADE и СDE (рис.) перпендикулярны к плоскости основания, то ребро DE есть высота пирамиды.

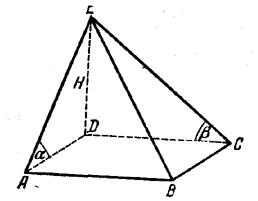
Угол DAE есть линейный для двугранного угла ЕАВС, так как плоскость DAE перпендикулярна к ребру АВ (доказать!). Следовательно, ∠ DAE = α; аналогично ∠ DCE = β . Из треугольников ADE и СDЕ, где DE=H, находим AD и DC и подставляем в формулу

V = ¹/₃ AD • DC • Н.

Ответ: V = ¹/₃ Н³ ctg α ctg β.