Основанием пирамиды служит квадрат. Две противоположные грани — равнобедренные треугольники, одна из них образует с основанием внутренний угол β, а другая — внешний острый угол α. Высота пирамиды равна Н. Найти объем пирамиды и углы, образованные двумя другими боковыми гранями с плоскостью основания.
Грани ADE и ВСЕ (рис.) - равнобедренные треугольники.
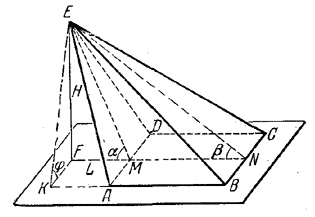
Плоскость EMN (М и N- середины ребер AD и ВС) перпендикулярна к ВС и AD и проходит через высоту EF пирамиды (доказать!).
По условию внешний угол α = ∠ EML треугольника EMN - острый. Поэтому высота EF пересекает продолжение MN. Чтобы определить V, найдем сторону АВ квадрата ABCD. Имеем
AB = MN =NF - MF = H (ctg β - ctg α).
Следовательно,
V = 1/3 АВ2 • Н = 1/3 Н3(ctg β - ctg α)2
Построим линейный угол φ двугранного угла, под которым грань ABE наклонена к основанию. Для этого пересечем двугранный угол плоскостью EFK, перпендикулярной к ребру АВ. Чтобы изобразить ее, надо провести FK || AD до пересечения с продолжением ребра АВ (доказать!). Из треугольника EFK находим
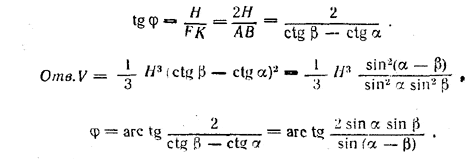
Похожие примеры: