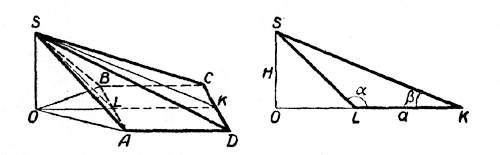
Пусть ABCD - основание пирамиды; S - вершина; OS - высота: ASB - грань, образующая с основанием угол \(\alpha\); DSC - грань, образующая с основанием угол \(\beta\).
Наклонные SA и SB равны; поэтому их проекции О А и ОВ на плоскость основания равны. Пусть L - середина стороны АВ. В равнобедренных треугольниках АОВ и ASB медианы OL и SL -также и высоты; поэтому OL \(\perp\) АВ и SL \(\perp\) АВ. Следовательно, \(\angle\)OLS есть линейный угол двугранного угла OABS (с ребром АВ), а потому \(\angle\)OLS = 180° - \(\alpha\). Пусть K- точка пересечения прямой OL со стороной CD; имеем: DK = KС и ОK \(\perp\) CD. Наклонная SK \(\perp\) CD пo теореме о трёх перпендикулярах. Так как OK \(\perp\) CD и SK \(\perp\) CD, то \(\angle\)OKS = \(\beta\). Полуплоскости ABS и DCS пересекутся в том и только в том случае, если

180° - \(\alpha\) > \(\beta\), т.е. \(\alpha\)+\(\beta\) < 180°

(угол 180°- \(\alpha\) есть внешний угол треугольника SLK, а \(\beta\)- внутренний угол); это условие будем считать выполненным. Отрезок LK равен стороне основания a. Так как OL = Hctg (180° - \(\alpha\)) = - Hctg \(\alpha\)(из треугольника SOL) и ОK= Hctg \(\beta\)(из треугольника SOK), то a = ОK - OL = H(ctg \(\beta\)+ ctg \(\alpha\)). Вычисляем объем: $$ V = \frac{1}{3}\alpha^2 H = \frac{1}{3}H^3(ctg\beta + ctg\alpha)^2 $$

Эта форма ответа удобна для вычислений с помощью натуральных таблиц. Если вычисления проводятся при помощи логарифмических таблиц или линейки, то следует сумму котангенсов преобразовать в произведение:

$$ V = \frac{1}{3}H^3\frac{sin^2(\alpha + \beta)}{sin^2 \alpha sin^2 \beta} $$

Например, вычислим объём при следующих данных: Н ≈ 12,53; α≈110°48': β= 32°30'.

1) Н³ ≈(12,53)³ ≈1967 (таблица V Брадиса).

2) ctg β+ ctg α≈ctg 32630' + ctg 110°48' = ctg 32°30' - ctg 69°12' ≈1,5697 - 0,3799 ≈ ≈1,1898 ≈1,190 (таблица IX Брадиса).

3) (ctg β+ ctg α)² ≈(1,190)² ≈1,416 (таблица III Брадиса) и, наконец,

$$ V = \frac{H^3(ctg\beta + ctg\alpha)^2}{3} \approx \frac{1967 \cdot 1,416}{3} \approx 928,4 $$