Диагональ прямоугольного параллелепипеда, равная d, образует с боковой гранью угол β= 90°— α. Плоскость, проведенная через эту диагональ и боковое ребро, пересекающееся с ней, образует с той же боковой гранью угол α(доказать, что α > 45°). Определить объем параллелепипеда.

Проекцией диагонали D₁B на боковую грань AA₁D₁D (рис.) будет AD₁, поэтому ∠ AD₁В = β.

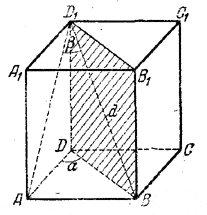
Угол α между плоскостью сечения DBB₁D₁ и плоскостью грани ADD₁A₁ измеряется углом ADB (доказать!). Из треугольника AD₁B находим AВ и AD₁ из треугольника ABD находим AD и из треугольника AD₁D находим DD₁ = H;

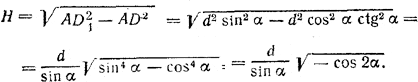
Замечание. Угол β всегда меньше угла α (сравнить их тангенсы!). Так как по условию β = 90° - α, то 90° - α < α, следовательно, α >45°. Из неравенства

45°< α < 90°

следует, что угол 2α принадлежит второй четверти, так что cos 2α < 0, a - cos 2α > 0. Для вычислений удобнее заменить - cos 2α выражением cos (180°-2α), так как угол 180°-2α принадлежит первой четверти.

Ответ: V = d³ cos α ctg² α √cos (180° - 2α).