В правильной треугольной призме две вершины верхнего основания соединены с серединами противоположных им сторон нижнего основания. Угол между полученными линиями, обращенный отверстием к плоскости основания, равен α. Сторона основания равна b. Определить объем призмы.
Проведенные линии суть A1N и В1М (рис.).
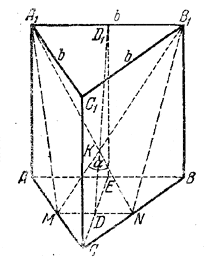
Четырехугольник A1B1NM - равнобочная трапеция (доказать!). Из равнобедренного треугольника MKN, где ∠ MKN = α и MN = b/2 имеем
KD = b/4 ctg α/2
Из треугольника A1KВ1 находим
KD1 = b/2 ctg α/2
Складывая эти равенства, получаем
DD1 = 3b/4 ctg α/2
Из треугольника DED1, где DE = 1/2СЕ = 1/4 b√3, находим
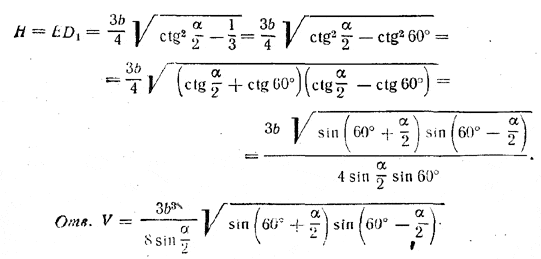
Похожие примеры: