Основанием пирамиды служит равнобедренный треугольник с углом αпри основании. Каждый из двугранных углов при основании равен φ. Расстояние от центра круга, вписанного в основание пирамиды, до середины высоты боковой грани равно d. Определить полную поверхность пирамиды.
По условию EO = d (рис.).
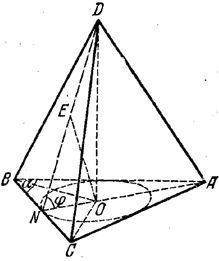
Точка Е (середина гипотенузы ND треугольника NOD) есть центр окружности, описанной около треугольника NOD. Поэтому ND = 2 • ED = 2 • EO = 2d.
Из треугольника DON, где ∠ OND = φ, находим радиус ON= r круга, вписанного в основание: r = 2d cos φ. Чтобы найти Socн. , определим BN (половину основания равнобедренного треугольника ABC) и AN (его высоту). Центр О вписанного круга лежит на биссектрисе угла ABC, равного α, т. е. ∠ OBN = α/2 Из треугольника BON находим BN = r ctg α/2.
Из треугольника ABN находим AN=BN • tg α. Следовательно,
Socн. = 1/2BC • AN = BN • AN = BN2• tg α = r2 ctg2 α/2 • tg α = 4d2 cos2φ ctg2 α/2 tg α.
Отсюда (см. задачу 429) найдем:
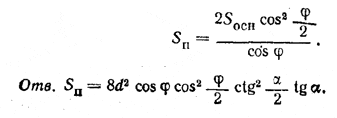
Похожие примеры: