В основании пирамиды лежит прямоугольный треугольник, у которого один острый угол равен αи радиус вписанного круга равен r. Каждая из боковых граней образует с основанием угол α. Определить объем, боковую и полную поверхность пирамиды.

Пусть r = ON - радиус круга, вписанного в основание пирамиды.

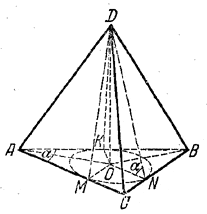
Из треугольника DON (рис.) имеем CO = H = r tg α. Так как центр О вписанной окружности лежит на пересечении биссектрис углов A и В, то

’Гак как угол С прямой, то четырехугольник MCNO - квадрат, так что MC = CN = r. Следовательно,

АС = b = AM + МС = r (ctg ^α/₂ + l) и СB = a = r [ctg (45° - ^α/₂) + 1] .

Выражения в скобках преобразуются, как в задаче 470, после чего получаем

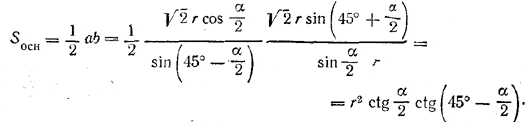
Следовательно,

V = ¹/₃ S_ocн. • H = ¹/₃ r³ tg α ctg ^α/₂ ctg (45° - ^α/₂ )

Это выражение можно упростить, если заметить, что

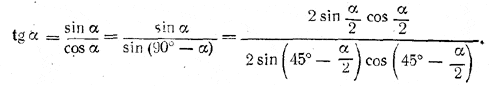
Боковую и полную поверхность можно найти по формулам

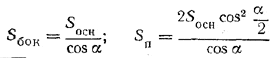
(См. задачу 425.)