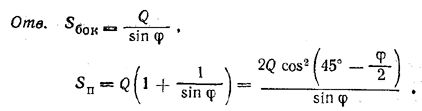В правильной n-угольной пирамиде площадь основания равна Q, а высота составляет с каждой из боковых граней угол φ. Определить боковую и полную поверхность пирамиды.
Если все боковые грани пирамиды наклонены к основанию под одним и тем же углом α, а высота проходит через некоторую точку О основания пирамиды, то- высоты всех граней равны;
- в основание пирамиды можно вписать окружность, центром последней будет точка О;
- Socн.= Sбок. cos α
Доказательство. 1) Проведем (рис.) высоту FM боковой грани BFC и соединим М с точкой О.
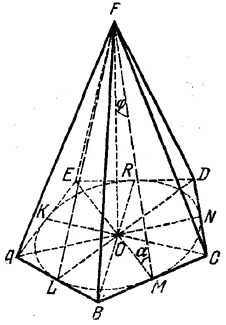
Отрезок ОМ есть проекция FM на плоскость ABCDE. Следовательно, он перпендикулярен к ВС («теорема о трех перпендикулярах»). Значит, угол OMF - линейный для двугранного угла α. Из треугольника OMF имеем
FM = OF/sin α ; ОМ = OF• ctg α.
Если из вершины F провести высоты FL, FN и высоты других боковых граней, то таким же образом найдем, что все они равны OF/sin α .
2) Отрезки OL, ОМ и т. д. будут перпендикулярны соответственно к сторонам АВ, ВС и т. д. и равны OF• ctg α. Поэтому если провести из центра О окружность радиуса ОМ, то она будет вписана в основание ABCDE.
3) Точка О - основание высоты пирамиды, по доказанному есть центр вписанной окружности.
4) SOBC = 1/2ВС • ОМ = 1/2 ВС (FM • cos α) = ( 1/2 ВС • FM ) cos α = SFBC cos α
Точно так же найдем, что SOAB = SFAB cos α и т. д.. Складывая эти равенства, получим Socн. = Sбок. cos α .
----------------------------------------------
Высота FO всякой пирамиды (рис.) проектируется на боковую грань BFC отрезком, лежащим на прямой FM.

Поэтому ∠ OFM = φ. Значит, α = 90° - φ, т. е. все грани наклонены к основанию под одним и тем же углом. По доказанному
Sбок. = Q/cos α = Q/sin φ