Боковое ребро правильной четырехугольной пирамиды, длиной m, наклонено к плоскости основания под углом α. Найти объем пирамиды.

Квадрат, лежащий в основании, изображается произвольным параллелограммом ABCD (рис.).

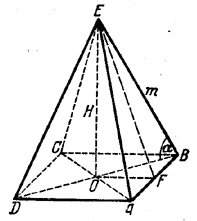
Точка О пересечения диагоналей изображает центр квадрата. Соединяя середину F стороны АВ с вершиной пирамиды К, получаем изображение EF апофемы.

б) Решение. Имеем

V = ¹/₃ х²Н,

где х - сторона основания (АВ на рис.) и H - высота пирамиды (ОЕ). Угол α есть ∠EBO (см. решение задачи 88).

Из треугольника EBO находим x = m sin α;

из треугольника ОАВ x = ОВ•√2 = m √2 • cos α.