В основании наклонной призмы лежит прямоугольный треугольник ABC, сумма катетов которого равна m и угол при вершине А равен α. Боковая грань призмы, проходящая через катет АС, наклонена к основанию под углом β. Через гипотенузу AВ и через вершину С1 противоположного трехгранного угла проведена плоскость. Определить объём отсеченной треугольной пирамиды, если известно, что боковые ребра ее равны между собой.
Требуется найти объем пирамиды C1ABC (рис.).
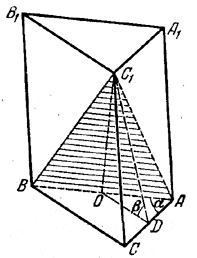
Так как боковые ребра ее равны между собой, то они наклонены к основанию под одним и тем же углом (эта теорема обратна доказанной в задаче 425 ), и высота С1О проходит через центр О окружности, описанной около треугольника ABC. Так как этот треугольник прямоугольный, то О лежит на середине гипотенузы АВ (см. объяснение к предыдущей задаче).
Угол ODC1 (В -середина катета АС) измеряет наклон боковой грани АСС1А1 к основанию. Катеты ВС и АС находим из двух уравнений:
ВС+АС = m и ВС = АС • tg α;
получаем
![]()
Затем находим Socн. = 1/2 ВС • AС. Высоту H находим из треугольника DOC1, где OD = 1/2BС (как средняя линия треугольника).
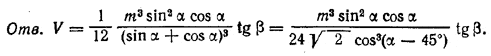
Похожие примеры: