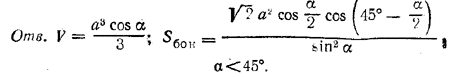В основании прямой призмы лежит прямоугольный треугольник с катетом а и противолежащим ему углом α. Через вершину прямого угла нижнего основания проведена плоскость, параллельная гипотенузе, под углом β= 90°— α к противолежащей боковой грани и пересекающая ее. Определить объем части призмы между ее основанием и сечением и боковую поверхность призмы, если известно, что боковая грань, проходящая через катет а, равновелика сечению призмы. Определить, при каком значении угла αплоскость сечения пересекает боковую грань, проходящую через гипотенузу основания.
Плоскость сечения ECD (рис.), параллельного гипотенузе АВ, пересекает плоскость грани АВВ1А1 по прямой ED, параллельной АВ.
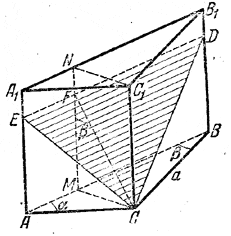
Опустив перпендикуляры СМ и CF на прямые АВ и ED, получим прямоугольный треугольник CMF, где ∠ CFM = β (доказать!) . Следовательно,
\(\Delta\)CMF = \(\Delta\)CMB
(у них общий катет МС и ∠ СВМ = 90°- α, а по условию β = 90°- α).
Требуется найти объем V пирамиды CABDE, у которой основание ABDE - прямоугольник, а высота равна СМ = a sin β = a cos α.
Имеем
V = 1/3• АВ • MF • СМ = 1/3• АВ • MB • CM = 1/3 • ВС2 • CM = 1/3 a3cos α
(катет ВС есть средняя пропорциональная между АВ и MB). Далее имеем
Sбок. = (ВС + AB + АС) Н = aH ( l + 1/sin α+ ctg α);
Здесь аН есть площадь грани СВВ1С1, которая по условию равна площади Scеч. треугольника CDE. Следовательно,
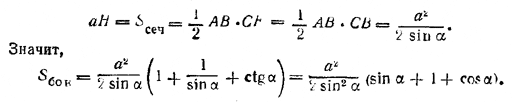
Выражение в скобках преобразуется, как в задаче 481.
Чтобы плоскость CDE пересекала грань ABB1A1, отрезок MF =MB = a sin α должен быть меньше, чем отрезок 
Из неравенства 
находим sin 2 α < 1/2 т. е sin α < √2/2. Значит, угол α должен быть меньше 45°.
