В основании прямой призмы лежит равнобочная трапеция с острым углом α, описанная около круга радиуса r. Через боковую сторону нижнего основания и противоположную вершину острого угла верхнего основания проведена плоскость, образующая с плоскостью основания угол α. Определить боковую поверхность призмы и площадь сечения.
Сначала начертим отдельно основание призмы (рис., а).
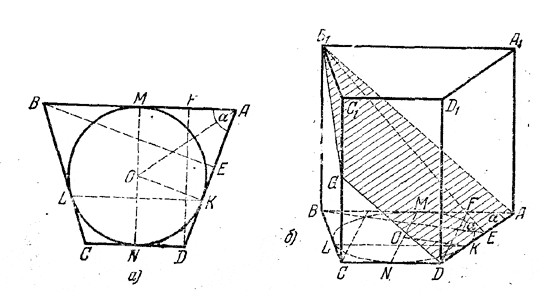
Затем проведем эллипс (рис., б), изображающий круг, около которого описано основание. Проведем какой-либо диаметр MN эллипса, и через концы его проведем касательные CD и АВ; они изображают прямые, на которых лежат основания равнобочной трапеции. Проводим какую-либо прямую KL, параллельную CD и АВ, Через точки К и L, в которых она пересекает эллипс, проводим касательные к эллипсу (DA и ВС). Четырехугольник ABCD изображает равнобочную трапецию, описанную около круга. Далее строим изображение прямой призмы ABCDA1B1C1D1. Секущая плоскость, проходящая через боковую сторону AD и вершину В1, пересечет грань АА1В1В по прямой AB1, а параллельную ей грань - по прямой DG, параллельной АВ1. В сечении получаем четырехугольник AB1GD. Из точки В проводим прямую BE, параллельную радиусу ОК, ведущему в точку касания К. Эта прямая изображает перпендикуляр, опущенный из В на AD. Следовательно, угол BEB1 есть изображение линейного угла α.
Решение. Из треугольника DFA (рис., б), где DF = MN = 2r и ∠ DAF = α, находим ВС = AD = 2r/sin α .
Обозначим АВ через a, CD - через b, AD = BC - через с. По свойству описанного четырехугольника
а + b = АВ + CD = AD + ВС = 2с = 4r/sin α .
Имеем
![]()
Следовательно,
![]()
Высоту H = BB1 найдем из треугольника ВВ1Е, предварительно определив BE из треугольника ВЕА, где
AB = a = 2AM=2OM • ctg ∠ OAM = 2r ctg α/2
Имеем
ВЕ = а sin α и Н = ВЕ • tg α.
Следовательно,
H = 2r ctg α/2 sin α tg α.
Теперь находим
Sбок. = H (а + b + 2с) = 4Hс.
![]()