В основании прямой призмы лежит четырехугольник, в котором два противолежащих угла прямые. Диагональ основания, соединяющая вершины непрямых углов, имеет длину l и делит один из этих углов на части αи β. Площадь сечения, проведенного через другую диагональ основания перпендикулярно к нему, равна S. Найти объем призмы.

1) Найдем площадь Q основания призмы (рис.).

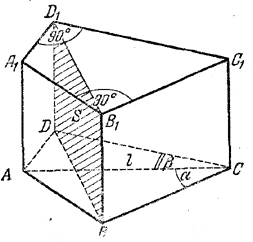
Имеем: Q = S₁ + S₂, где S₁ - площадь прямоугольного треугольника ABC, a S₂ - площадь прямоугольного треугольника ADC,

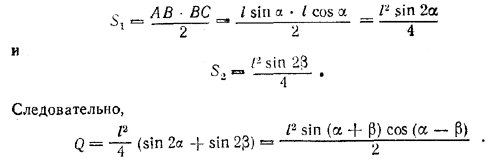
2) Найдем высоту Н призмы из условия S = BD • H. Так как в четырехугольнике ABCD сумма углов при вершинах В и D равна 180°, то около него можно описать окружность, диаметром которой будет диагональ АС, потому что на нее опираются прямые вписанные углы. Из треугольника BCD, вписанного в эту окружность, находим (по теореме синусов)

BD = AC • sin ∠ DCB = l sin (α + β),

Следовательно,

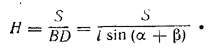
Ответ: V = ¹/₂ S • l cos (α - β).