Основание четырехугольной пирамиды — прямоугольник с диагональю, равной b, и углом αмежду диагоналями. Каждое из боковых ребер образует с основанием угол β. Найти объем пирамиды.

Если все боковые ребра пирамиды образуют равные углы с основанием, то

1. все боковые ребра равны;
2. около основания можно описать окружность;
3. высота пирамиды проходит через центр этой окружности.

Доказательство. Пусть ребра SA, SB, SC и т. д. (рис.) образуют с плоскостью ABCDE равные углы.

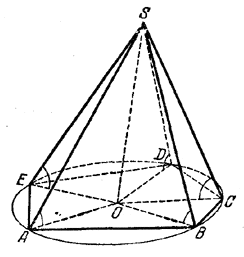
Рассмотрим прямоугольные треугольники AOS и BOS (OS - высота пирамиды). У них общая высота, а острые углы OAS и OBS равны (так как они измеряют углы наклона ребер SA, SB к основанию). Следовательно, AS = BS. Так же докажем, что BS = CS и т. д. Из тех же треугольников AOS и BOS находим АО = ОВ. Так же докажем, что ОВ = ОС и т. д. Значит, окружность с центром в О и радиусом ОА пройдет через точки В, С и т. д.

------------------------------------------------

По доказанному, высота ЕО проходит через центр описанной окружности, т. е. через точку О пересечения диагоналей (рис.).

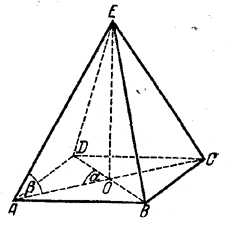
Площадь всякого параллелограмма равна половине произведения диагоналей на синус угла между ними. Поэтому S_ocн. =¹/₂ b²sin α . Из треугольника АОЕ находим:

H = AO • tg β = ^b/₂ tg β

Ответ: V = ¹/₁₂ b³sin α tg β