Основанием пирамиды служит равнобедренный треугольник с боковыми сторонами, равными а, и углом между ними, равным α. Все боковые ребра наклонены к основанию под углом β. Определить объем пирамиды.
Высота пирамиды должна проходить через-центр окружности, описанной около равнобедренного треугольника ABC (рис.).
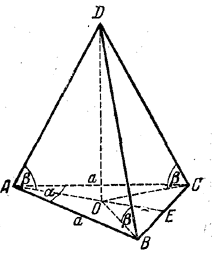
Поскольку угол α = ∠CAB при вершине остается произвольным, изображение центра О можно взять в любой точке отрезка АЕ (Е - середина ВС) и даже на продолжении его за точку Е (в последнем случае угол α в натуре тупой).
Решение. Высоту DO определим из треугольника AOD, где ∠OAD = β, a AO = R есть радиус описанной окружности. Согласно теореме синусов сторона ВС равна произведению диаметра 2R описанной окружности на синус противоположного угла α , так что ![]()
Вeличина BC/2 = ВE находится из треугольника ABE ( BC/2 = a sin α/2)
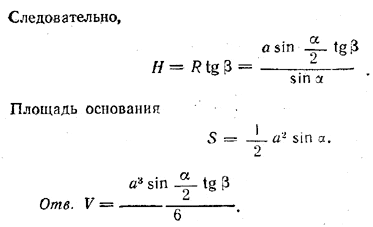
Похожие примеры: