Основанием прямоугольного параллелепипеда служит прямоугольник, вписанный в круг радиуса R, причем меньшая сторона этого прямоугольника стягивает дугу окружности, содержащую (2α)°. Найти объем этого параллелепипеда, зная его боковую поверхность S.

Окружность изображается в параллельной проекции эллипсом.

Эллипс можно построить следующим образом.

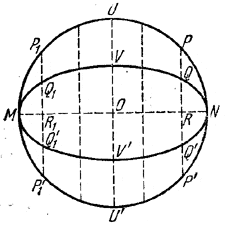
Проведем какой-либо диаметр MN окружности (рис.) и из произвольной точки Р окружности проведем прямую РР’, перпендикулярную к MN. Пусть R - точка пересечения РР’ с M.N. Укоротим отрезок RP в каком-либо отношении (например вдвое) и отложим укороченный отрезок RQ на той же прямой РР’ по обе стороны от R (RQ = RQ’). Поступая так с рядом точек окружности, получим ряд тoчек эллипса.

Эллипс симметричен относительно MN (большая ось эллипса) и относительно прямой UU’, проведенной через центр О перпендикулярно к MN (отрезок VV’ - малая ось эллипса). Точка О называется центром эллипса.

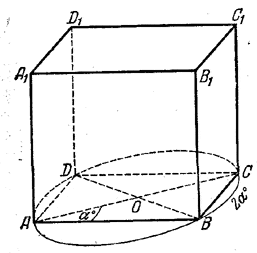
Чтобы изобразить окружность, описанную около прямоугольника, удобнее сначала начертить эллипс ABCD, изображающий описанную окружность (рис.).

(На рис. большая ось эллипса принята за диагональ АС прямоугольника. Это упрощает чертеж, но не является обязательным. )

При этом большую ось эллипса лучше расположить наклонно. Одну сторону прямоугольника можно изобразить произвольной хордой АВ эллипса; эту хорду целесообразно провести горизонтально. Через центр О эллипса проводим прямые BD и АС. Четырехугольник ABCD есть изображение прямоугольника.

Решение. Вписанный угол CAB содержит α°, так как опирается на дугу ВС в (2α)°. Из треугольника ВАС имеем АВ = 2R cos α; BC-2R sin α, так что

S = 2(AB+BC)H = 4R (cos α + sin α) H.

Отсюда

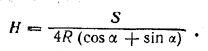
Теперь находим V=AB • BC • H. Условие, что дуга (2α)° стягивается меньшей стороной прямоугольника, является излишним.