К кругу радиуса R проведены из одной точки две касательные, составляющие между собой угол 2α. Определить площадь между этими касательными и дугой круга.

Площадь S₁ четырехугольника АВОС (рис.) равна 2• ¹/₂ОВ • AB = R² ctg α.

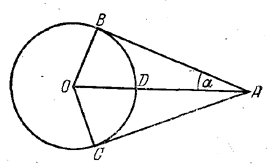
Из нее нужно отнять площадь S₂ сектора COBD, центральный угол которого равен (180 - 2α)°. Имеем

(α - градусная мера).

Ответ: S = S₁- S₂ = R² [ctg α - ^π/₂ + ^πα/₁₈₀], где α - градусная мера угла или

S = R² [ctg α - ^π/₂ + α’], где α’- радианная мера угла.