В основании пирамиды лежит прямоугольный треугольник, являющийся проекцией боковой грани, проходящей через катет. Угол, лежащий против этого катета в основании пирамиды, равен α, а лежащий в боковой грани равен β. Площадь этой боковой грани больше площади, основания на S. Определить разность между площадями двух других граней и углы, образованные боковыми гранями с плоскостью основания.
Так как треугольник AВС (рис.) есть проекция треугольника DBC, то DA есть перпендикуляр к плоскости основания.
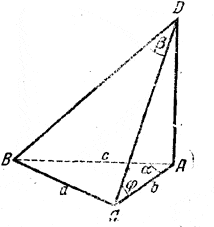
Площадь S1треугольника ABС равна
S1 = 1/2 ab = 1/2 a2 ctg α
Плошадь S2 треугольника BCD равна
S2 = 1/2 a2 ctg β.
По условию
1/2 a2 ( ctg β - ctg α ) = S ,
откуда ![]()
Площадь S3 грани DAС равна
S3 = 1/2 bH,
а площадь S4 грани DAB равна S4 = 1/2 cH.
Следовательно,
S4 - S3 = 1/2 H (с - b) = 1/2 aH (cosec α - ctg α).
Высоту Н определим из треугольника ACD; получим
Н = √DC2 - АС2 = √a2ctg2 β - a2ctg2 α
Следовательно,
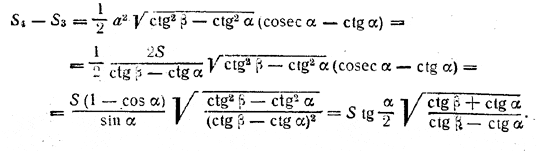
Боковые грани ADC и ADB образуют с основанием прямые углы. Грань BDC образует с основанием угол, измеряемый линейным углом DCA = φ;
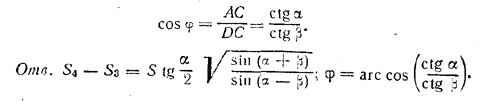
Похожие примеры: