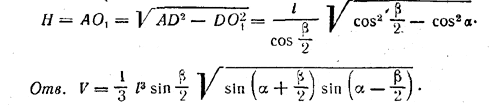Боковые ребра треугольной пирамиды имеют одинаковую длину l . Из трех плоских углов, образованных при вершине пирамиды этими ребрами, два равны α, а третий равен β. Найти объем пирамиды.

Высота DO проходит через центр О (рис., а) круга, описанного около треугольника ABC, где AB = AС = 2l sin ^α/₂ и ВС = 2l sin ^β/₂ (См.задачу 419).

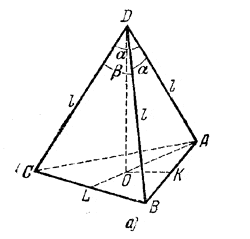
рис., а

Точка О лежит на перпендикуляре KО к стороне AВ, проведенном через середину AВ. Поэтому из подобия треугольников АОК и ABL имеем пропорцию

АО : ¹/₂ AB= АВ : AL,

откуда

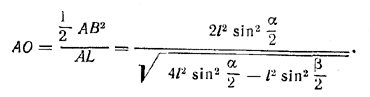
Далее из треугольника AOD находим

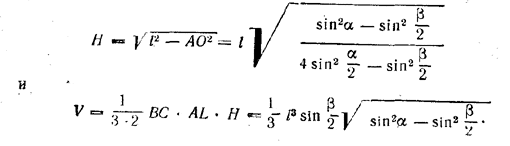
Подкоренное выражение можно преобразовать, как указано в задаче 464.

Другой способ. Примем за основание пирамиды грянь BDC (рис., б);

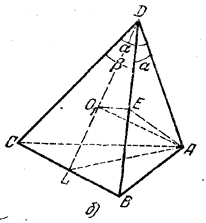
рис., б

площадь ее S_ocн. = ¹/₂ l² sin β. Грань BDC перпендикулярна к плоскости ADL (доказать!) и, следовательно, высота пирамиды АО₁ будет лежать в этой плоскости. Проводим О₁Е перпендикулярно к BD. Из подобия треугольников O₁DE и BDL имеем , где из \(\Delta\)ADE

ED = l cos α , BD = l и DL = l cos ^β/₂

отсюда

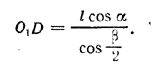
Из треугольника ADO₁ находим