В прямоугольном параллелепипеде точка пересечения диагоналей нижнего основания соединена с серединой одного из боковых ребер прямой, длина которой равна m. Она образует с основанием угол α и с одной из боковых граней угол β = 2α. Приняв другую смежную боковую грань за основание параллелепипеда, найти его боковую поверхность и объем. (Доказать, что α < 30°.)

Угол ЕОС = α (рис.).

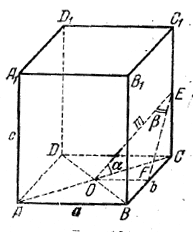
Для построения угла β отрезка ОЕ с боковой гранью ВВ₁С₁С проведем OF⊥BC. Проекцией ОЕ на эту грань будет FE, так что ∠ OEF = β.

Если обозначим АВ = а; ВС = b и СС₁ = с, то V = аbс и S_бок. = 2 (а + с) b.

Из \(\Delta\)OEF имеем

^a/₂ = ОF = m sin β = m sin 2α;

FE = m cos β = m cos 2α;

из \(\Delta\)OEC имеем

^c/₂ = EC = m sin α;

из \(\Delta\)FEC имеем

^b/₂ = FC = √FE² - EC² = m √cos²2α - sin²α.

Приведем подкоренное выражение к виду, удобному для логарифмирования:

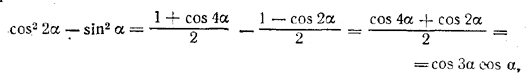
Следовательно,

b = 2m √cos 3α cos α

Замечание. Угол β = ∠ OEF меньше, чем ∠ OEC = 90°- α (сравнить их синусы!). А так как по условию β =2α, то 2α < 90°- α. Следовательно, должно быть α < 30°.

Ответ: V = 8m³ sin 2α sin α √cos 3α cos α;

S_бок. = 16m² sin ^3α/₂ cos ^α/₂ √cos 3α cos α.