Диагональ прямоугольного параллелепипеда равна dи образует с двумя смежными боковыми гранями равные углы α. Определить объем параллелепипеда и угол, который образует с плоскостью основания плоскость, проведенная через концы трех ребер, выходящих из одной вершины.
Имеем (рис.) ∠ ВD1A= α и ∠ BD1C = α (доказать!).
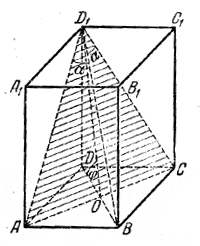
Треугольники BD1A и BD1C равны (доказать!). Следовательно, основание ABCD - квадрат со стороной a = d sin α. Далее находим
AD1= d cos α
и
H =√AD12 - AD2 = √d2 cos2 α - d2 sin2 α = d √cos 2α.
Плоскость ACD1 образует с плоскостью основания угол φ = ∠ DOD1.
tg φ = DD1/OD = H : a/√2
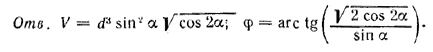
Похожие примеры: