Через сторону основания правильной треугольной пирамиды проведена плоскость перпендикулярно к противолежащему боковому ребру. Определить полную поверхность пирамиды, если указанная плоскость делит боковое ребро в отношении m : n и сторона основания равна q.
Для вычисления полной поверхности неизвестна только апофема ND. Для определения ее найдем сначала отрезки AM и MD (рис.), на которые делится ребро AD перпендикулярной к нему прямой NM (N - середина ВС).
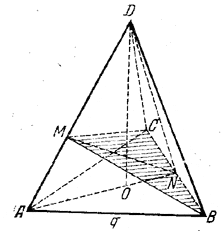
Затем из треугольника ANM, где AN = q√3/2, найдем MN и, наконец, из треугольника NMD найдем ND.
В условии не сказано, какое из двух отношении - AM : MD или MD : AM - равно m : n, поэтому можно положить MD = mx, MA= nx, так что AD= (т + п)х. Из подобия треугольников AMN и ADO имеем
АM/AO= АN/AD ,
где
AN = q√3/2
и
AO = 2/3AN = q√3/3
Получаем уравнение
пх • (т + п) х = q√3/2 • q√3/3
Отсюда находим
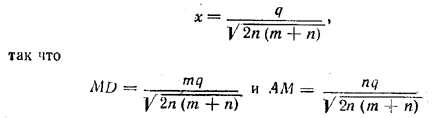
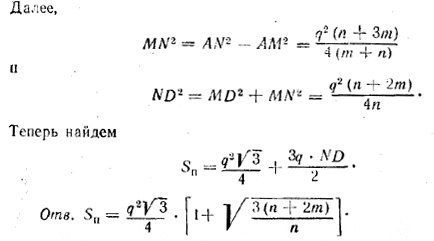
Похожие примеры: