Треугольник ABC вписан в окружность; через вершину А проведена касательная до пересечения с продолженной стороной ВС в точке D. Из вершин В и С опущены перпендикуляры на касательную, меньший из которых равен 6 см. Определить площадь трапеции, образованной этими перпендикулярами, стороной ВС и отрезком касательной, если ВС = 5 см, AD = 5√6см.

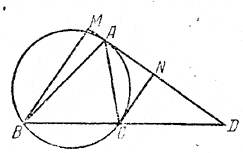
Чтобы найти площадь трапеции BMNC (рис.), нужно найти основание ВМ и высоту MN, так как CN известно.

Определим сначала

CD = x.

Имеем

x (BC + x) =AD²

или

x (5 + x) = 150.

Отсюда

CD = x = 10 (см).

Из подобия треугольников BMD и СND следует ^BM/_ВD = ^CN/_CD или ^BM/₁₅ = ⁶/₁₀ откуда ВМ = 9 (см).

Высоту MN трапеции найдем из пропорции ^MN/_EC = ^ND/_CD , где ND = √CD² - CN² Получим MN = 4 см.

Ответ: S = 30 см².