В правильный треугольник, сторона которого равна а, вписаны три равных круга, касательных друг к другу. Каждый из них касается двух сторон данного треугольника. Определить радиусы этих кругов.
Пусть O1, О2 и О3 - центры равных вписанных кругов и пусть r - их радиус (рис.).
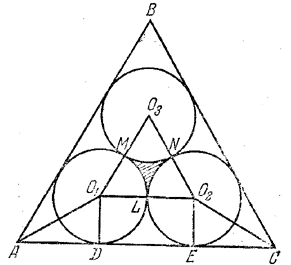
Так как АО1 и СО2 - биссектрисы углов А и С, равных 60°, то ∠О1AD = 30°; следовательно, AD = ЕС = r√3 . Далее DE = О1О2 = 2r Поэтому 2r (1 + √3) = а.
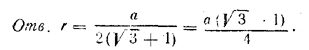
Похожие примеры: