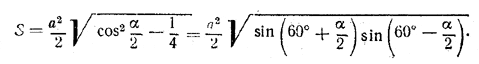В правильной треугольной пирамиде со стороной основания, равной а, углы между ребрами при ее вершине равны между собой и каждый равен α(α <90°). Определить углы между боковыми гранями пирамиды и площадь сечения, проведенного через сторону основания перпендикулярно к противолежащему боковому ребру.
Плоскость ВСE (рис.) проведена через сторону ВС перпендикулярно к ребру AS. Двугранные углы между боковыми гранями (все они равны) измеряются углом ВEС = φ. Треугольник ВЕС - равнобедренный.
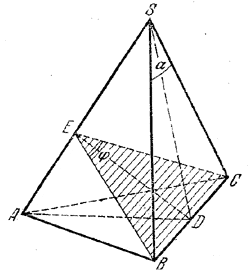
Чтобы определить площадь S сечения и угол φ, достаточно найти DE (D - середина ВС). Для этого последовательно находим BS (из треугольника BSD, где BD = a/2 и ∠ BSD = α/2 ).
Затем BE (из треугольника BSE, где ∠BSE = α) и, наконец, DE=√BE2-BD2 . Получаем
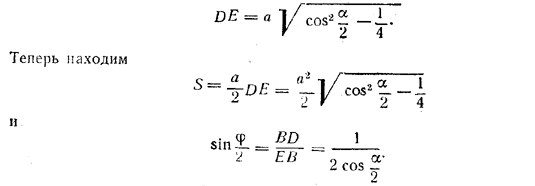
Замечание 1. Сумма плоских углов при вершине S всегда меньше 360°. Поэтому 0<α<120°. При этом условии 2cosα/2> 1, т. е.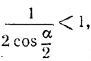
так что уравнение 
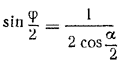всегда имеет решение.
Замечание 2. Если α>90°, т. е. угол ASB при вершине боковой грани тупой, то высота BE треугольника ASB пересечет продолжение основания, и плоскость ВЕС не даст никакого сечения пирамиды. Между тем формула
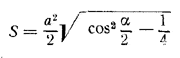
и при тупом угле α (меньшем 120°, см. замечание 1) даст определенное значение S.
Ответ: φ = 2 arc sin ( 1/2 sec α/2);
