Пирамида имеет в основании прямоугольный треугольник с катетом а. Одно из боковых ребер пирамиды перпендикулярно к плоскости основания, а другие два наклонены к ней под одним и тем же углом α. Плоскость, перпендикулярная к основанию, дает в сечении с пирамидой квадрат. Определить площадь этого квадрата.
Пусть CD (рис.) есть боковое ребро, перпендикулярное к плоскости основания. Так как по условию ∠ DAC = ∠ DBC = α , то АС = СВ, т. е. треугольник ABC - равнобедренный при вершине С и, значит, по условию ∠ C = 90°.
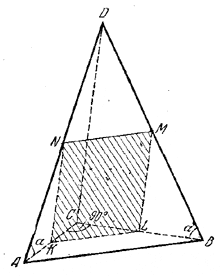
Всякое сечение пирамиды, перпендикулярное к основанию ABC, есть четырехугольник NKLM с двумя прямыми углами (∠ NKL и ∠ KLM). Чтобы этот четырехугольник был квадратом, должно быть KN=KL = LM = x. Из равенства треугольников AKN и BLM (доказать!) следует, что AK = BL, значит, KC = CL, так что КС = KL/√2 = x/√2
Из треугольника AKN находим AK = KN • ctg α = x ctg α, так как КС + АК = АС = а, то получаем уравнение
x/√2 + x ctg α = а.
откуда
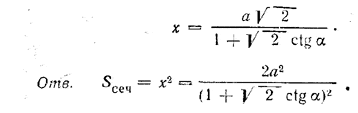
Похожие примеры: