Правильная треугольная пирамида рассечена плоскостью, перпендикулярной к основанию и делящей две стороны основания пополам. Определить объем отсеченной пирамиды, если даны сторона а основания первоначальной пирамиды и двугранный угол αпри основании.
Чтобы изобразить сечение, перпендикулярное к основанию ABC (рис.) и делящее пополам стороны основания АВ и АС, проведем среднюю линию MN.
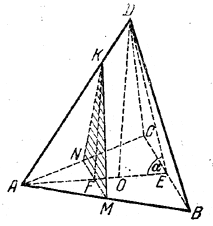
Из точки F, где MN пересекает медиану АЕ, проведем FK параллельно высоте OD. Искомое сечение есть NMK. Действительно, плоскость NMK проходит через прямую FK., перпендикулярную к плоскости ABC (значит, плоскость NMK перпендикулярна к плоскости ABC). Двугранный угол α измеряется углом AED (доказать!).
Плоскость AED проходит через прямую KF, так как точки K и F лежат в плоскости AED.
Решение. Примем за основание пирамиды KANM треугольник AMN. Его площадь S составляет 1/4 площади треугольника ABC, т. е. S =1/16 a2√3. Высоту KF выразим через OD, пользуясь подобием треугольников AFK и AOD. Так как AF составляет 3/4 АО (ибо AF = 1/2 АЕ, а АО = 2/3AE) , то KF = 3/4 OD.
Отрезок OD находим из треугольника DOE, где OЕ = a√3/6 и ∠ DEO = α.
![]()