Пирамида имеет в основании равнобедренный треугольник; боковые стороны этого основания равны а и образуют угол в 120°. Боковое ребро пирамиды, проходящее через вершину тупого угла, перпендикулярно к плоскости основания, а остальные два наклонены к ней под углом α. Определить площадь сечения пирамиды плоскостью, которая проходит через наибольшую сторону основания пирамиды и делит пополам ребро, перпендикулярное к основанию.

Площадь S сечения равна ¹/₂ •AB•NM (рис.).

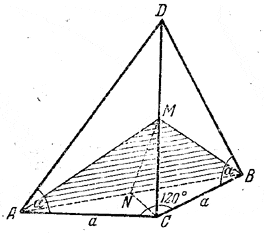
Из прямоугольного треугольника AСN, где ∠ CAN=30°, находим

AN = ¹/₂ •AB = ^√3/₂ a и CN = ¹/₂ a

Из треугольника NСM имеем

где H = а tg α можно получить из треугольника AСD.