Показать, что площадь любого треугольного сечения произвольной треугольной пирамиды не превосходит площади хотя бы одной из ее граней.

Проведем сначала одно вспомогательное рассуждение. Пусть РР₁ и QQ₁ - две скрещивающиеся прямые, А, В и С-три точки на прямой QQ₁, причем точка В лежит между точками А и С, А₁, B₁, С₁- основания перпендикуляров, опущенных из точек А, В, С на прямую РР₁. Обозначим через h_A, h_B, h_C расстояния точек A, В и С от прямой РР₁ . Докажем, что h_B меньше, по крайней мере, одного из расстояний h_A или h_C.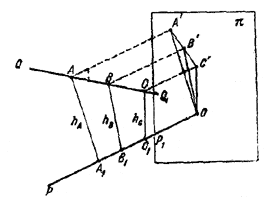

Для этого спроектируем изображенную на рис. фигуру на плоскость π, перпендикулярную к прямой РР₁. Тогда прямая PP₁ спроектируется в точку О, а отрезки АА₁, BB₁ и СС₁ спроектируются без изменения длины, так как все они параллельны плоскости π. При этом точка В' окажется между точками А' и С'.

Обращаясь теперь к треугольнику А'ОС', мы можем утверждать, что наклонная ОВ' короче одной из наклонных ОА' или ОС'. Действительно, опустив еще из точки О перпендикуляр на А'С' (на рис. он не показан), мы установим, что точка В' расположена ближе к основанию перпендикуляра, чем одна из двух других точек А' или С'. Отсюда уже следует, что h_B меньше, чем h_A или h_C.

Пусть теперь ABCD - произвольная треугольная пирамида и EFG -такое треугольное сечение, что, по крайней мере, одна из вершин F не является вершиной пирамиды. Докажем, что тогда площадь треугольника EFG меньше площади одного из треугольников AEG или DEG.

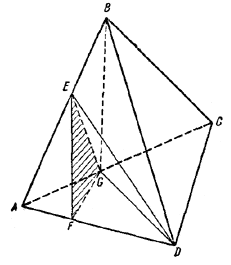
Действительно, все три треугольника имеют общую сторону EG, а по ранее доказанному расстояние от F до прямой EG меньше расстояния от А или D до этой прямой. Если S_{/\ EFG} < S_{/\ AEG} , то все доказано. Если же S_{/\ EFG} < S_{/\ DEG} и, например, точка Е не является вершиной пирамиды, то применим предыдущее рассуждение к \(\Delta\)DEG, сравнивая его площадь с площадями треугольников DGA и BDG. Применив то же самое рассуждение в случае необходимости еще раз по отношению к \(\Delta\)BDG, докажем утверждение, содержащееся в задаче. Из изложенного решения ясно, что если сечение пирамиды не совпадает с ее гранью, то оно по площади строго меньше площади одной из граней.