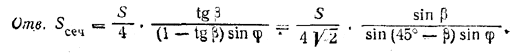В основании прямой призмы ABCA₁B₁C₁ лежит прямоугольный треугольник ABC с углом β при вершине В (β < 45°). Разность между площадями ее боковых граней, проходящих через катеты ВС и АС, равна S. Найти площадь сечения призмы плоскостью, образующей с плоскостью основания угол φ и проходящей через три точки: вершину В₁ угла β верхнего основания, середину бокового ребра АА₁ и точку D, расположенную на плоскости основания симметрично с вершиной В относительно катета АС.

Продолжив отрезок ВС (рис.), изображающий катет основания, на расстояние CD = ВС, получаем точку D, которая в натуре симметрична с В относительно катета АС.

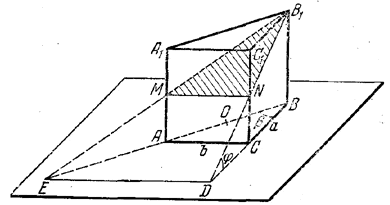
Возьмем точку М на середине ребра АА₁ и изобразим сечение призмы плоскостью Р, проходящей через точки В₁, M и D, Для этого соединим точки В, и D. В пересечении с ребром CC₁ найдем точку N. Треугольник B₁NM будет искомым сечением. Действительно, точка D лежит на прямой ВС и, значит, принадлежит плоскости СВВ₁С₁ (D находится на продолжении грани CBB₁C₁). Но точка D лежит также и на плоскости Р, поэтому она находится на линии пересечения плоскости Р с СВВ₁С₁.

Точно так же и точка B₁ находится на этой линии. Значит, плоскости Р и BCC₁B₁ пересекаются по прямой B₁D. Точка N, где B₁D пересекается с ребром СС₁, есть одна из вершин сечения, так что сечение призмы есть треугольник B₁NM.

Так как BC=CD и CN||BB₁ то CN есть средняя линия треугольника BB₁D, т. е. N- середина ребра СС₁. Следовательно, прямая MN параллельна прямой АС, лежащей, в плоскости основания. Вследствие этого и прямая DE, по которой плоскость Р пересечет плоскость основания, параллельна АС и, значит, перпендикулярна к плоскости грани ВСС₁В₁. Поэтому ∠ BDB₁ есть линейный дтол двугранного угла φ при ребре DE.

Решение. Имеем (см. решение задачи 516)

(где а = ВС, b = АС), а так как b = a tg β, то

Найдем а². По условию β есть меньший из острых углов треугольника ABC, так что b < a и площадь bН грани ACC₁A₁ меньше плошади аН грани ВСС₁В₁ Поэтому разность S этих площадей (предполагаем, что она положительна) равна (а-b)H. Из треугольника DBB₁, где BD =2BC = 2a, находим Н = 2а tg φ. Следовательно,

S=2а² (l - tg β) tg φ.

Отсюда находим а².