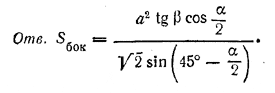В основании наклонной призмы лежит прямоугольный треугольник ABC с катетом ВС = а. Вершина В₁верхнего основания проектируется на середину катета ВС. Двугранный угол, образованный боковыми гранями, проводящими через катет ВС и гипотенузу АВ, равен α. Боковые ребра наклонены к плоскости основания под углом β. Определить боковую поверхность призмы.

На рис. отрезок АВ изображает гипотенузу основания. Для построения линейного угла а нужно пересечь ребро ВВ₁ плоскостью, перпендикулярной к этому ребру. В данном случае такую плоскость можно провести через катет АС. Чтобы доказать это, нужно доказать, что AC⊥BB₁

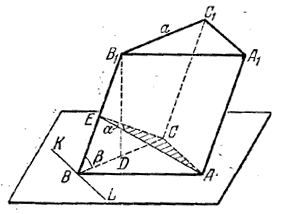
По условию вершина В₁ проектируется в точку D (середина ВС), лежащую на катете ВС.

Следовательно, если провести через В прямую KL, перпендикулярную к ВС, то KL будет перпендикулярна также и к BB₁ (теорема о трех перпендикулярах). А так как AC||KL, то AC⊥BB₁, что и требовалось доказать.

Проведем через АС плоскость АЕС, перпендикулярную к BB₁. Боковая поверхность призмы равна периметру СE + AC + AE перпендикулярного сечения, умноженному на ребро ВВ₁. Из прямоугольного треугольника ВСЕ, где ∠ CBE = β (доказать!) и ВС= а, находим СE = а sin β. Прямая KL, а значит, и параллельная ей прямая АС перпендикулярна к грани BB₁C₁C Поэтому треугольник АСЕ - прямоугольный при вершине С. Значит, АС = СЕ tg α и АЕ = ^CE/_{cos α} , так что

СЕ + АС + АЕ = a sin β (l + tg α + ¹/_{cos α} )

Ребро BB₁ находим из треугольника BDB₁ где BD = ^a/₂. Получаем ВВ₁ = ^a/_{2cos β} , так что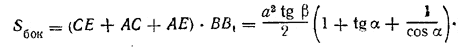

Преобразуем выражение в скобках, как указано в задаче 481, и cos α, как указано в задаче 489.