В основании прямой призмы лежит прямоугольный треугольник, у которого сумма катета и гипотенузы равна m и угол между ними равен α. Через другой катет и вершину противоположного трехгранного угла призмы проведена плоскость, образующая с основанием угол β. Определить объемы частей, на которые призма делится плоскостью сечения.
Одна из частей призмы есть треугольная пирамида В1АВС (рис.).
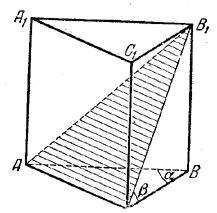
Ее объем V1 = 1/3V, где V - объем призмы. Значит, объем V2 другой части (четырехугольной пирамиды B1A1C1CA ) равен 2/3V
Найдем V.
По условию ВС + АВ = m, а из треугольника ABC находим BC=AB•cos α. Следовательно,
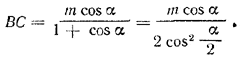
Площадь основания призмы S равна
S = 1/2 • АС • ВС = 1/2 • ВС2 • tg α.
Высоту Н = ВВ1 определяем из треугольника ВСВ1, где ∠ВСВ1 = β (доказать!). Получаем H = BC•tg β.
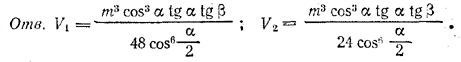
Похожие примеры: