В основании прямой призмы лежит равнобедренный треугольник с боковой стороной, равной а, и углом при основании, равным α. Через основание треугольника, являющегося верхней гранью, и противоположную вершину нижнего основания проведена плоскость, образующая с плоскостью основания угол β. Определить боковую поверхность призмы и объем отсеченной четырехугольной пирамиды.
Так как плоскость основания ABC (рис.) проходит через прямую АС, а плоскость сечения А1ВС1 - через прямую A1C1, параллельную АС, то ребро MN двугранного угла β параллельно прямым АС и A1C1.
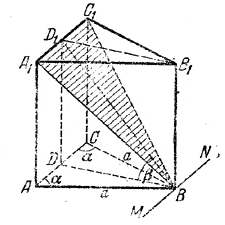
Поэтому для построения линейного угла проводим BD⊥AC и BD1⊥A1C1 (точки D и D1 будут серединами АС и A1C1). Имеем
Sбок. = (2AB + АС) • DD1 = (2AB + АС) • BD • tgβ = 2a2(1 + cos S) sin α tg β.
Объем V1 четырехугольной пирамиды BACC1A1 равен 2/3 объема V призмы (см. задачу 481) и, следовательно,
V1 = 2/3 S• DD1
где
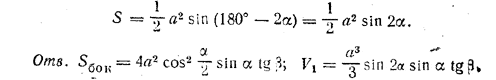
Похожие примеры: