В основании пирамиды — квадрат. Две боковые грани ее перпендикулярны к плоскости основания, а две другие наклонены к нему под углом α. Радиус круга, описанного около боковой грани, перпендикулярной к основанию, равен R. Определить полную поверхность пирамиды.

Как в задаче 438, докажем, что грань DCE (рис.) наклонена к плоскости основания ABCD под углом α =∠ ADE, a грань ВСЕ - под равным углом α = ∠ABE; обе эти грани - прямоугольные треугольники ( ∠CDE = ∠CBE = 90°).

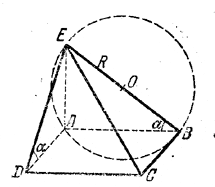
Площадь S₁ треугольника ADE (а также равная ей площадь треугольника ABE) равна S₁ = ¹/₂ AB • AE. Из треугольника ABE, где BE = 2R, находим

AB = 2R cos α, AE = 2R sin α,

так что S₁ = 2R² sin α cos α.

Площадь S₂ треугольника CDE (а также треугольника СВE) равна

S₂ = ¹/₂ BC • BE= ¹/₂ AB • BE = 2R² cos α.

Имеем

S_п. = S+2S₁+2S₂ = 4R²(cos²α + cos α sin α + cos α) = 4R²cos α (cos α +sin α +1).

Выражение в скобках преобразуется, как указано в задаче 481.

Ответ: S_п.= 8√2 R² cos α cos ^α/₂ cos (45° - ^α/₂)