Основанием прямой призмы служит прямоугольный треугольник с гипотенузой с и острым углом α. Через гипотенузу нижнего основания и вершину прямого угла верхнего основания проведена плоскость, образующая с плоскостью основания угол β. Определить объем треугольной пирамиды, отсеченной от призмы плоскостью.
Если СВ (рис.) есть высота треугольника ABC, опущенная на гипотенузу АВ = с ( на изображении можно провести CD произвольно внутри угла АСВ ), то ∠ CDC1 = β (доказать!).
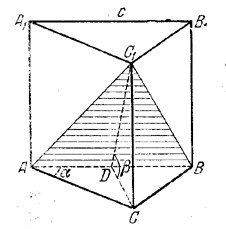
Имеем
CD = АВ • sin α cos α =1/2 с sin 2α
и
H = CC1 = CD • tg β
Эти выражения подставляем в формулу
V = 1/3SH =1/3 • 1/2 с • CD • H
Ответ: V = 1/24 с3 sin2 2α tg β.
Похожие примеры: