Определить объем правильной четырехугольной призмы, если ее диагональ образует с боковой гранью угол α, а сторона основания равна b.

Проекция диагонали BD₁(рис.) на боковую грань ВСС₁В₁ есть ВС₁.

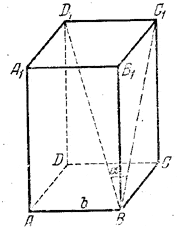
Поэтому ∠ C₁BD₁ = α. Из треугольника BC₁D₁, где D₁С₁= b, находим BC₁= b ctg α. Из треугольника В₁С₁В имеем

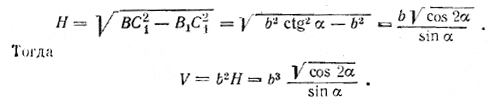
3амечание. Подкоренное выражение cos 2α здесь (ср. замечание 2 к задаче 446) всегда положительно, ибо α < 45°. Действительно,

По В₁С₁ есть катет, а ВС₁-гипотенуза треугольника ВВ₁С₁. Поэтому tg α < 1, т. е. α <45°.