Определить объем правильной усеченной четырехугольной пирамиды, если сторона большего основания равна а, сторона меньшего основания равна b, а острый угол боковой грани равен α.

Боковая грань ВСС₁В₁ (рис.) - равнобочная трапеция с основаниями ВС= а и B₁C₁ = b (a > b) и углом α при основании а.

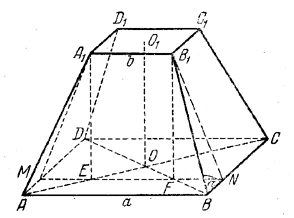
Отрезок B₁N - ее высота. Находим .

Из треугольника B₁NF, где , находим

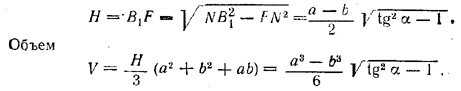
Замечание 1. Если острый угол a меньше чем 45°, подкоренное выражение отрицательно. Но угол α не может быть меньше 45°. Действительно, сумма плоских углов ВСС₁ = α п DCC₁ = α трехгранного угла С всегда больше третьего плоского угла BCD; но ∠ BCD = 90°, поэтому 2α > 90°, т. е. α > 45°.

Замечание 2. Выражение √tg²α - 1 можно преобразовать к виду

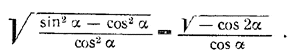
Так как 2α больше чем 90° (но меньше чем 180°, ибо α - острый угол), то cos 2αвсегда отрицателен. Значит, подкоренное выражение (- cos 2α) всегда положительно.