В точке А плоскости Р расположен источник света. Над плоскостью помещено полусферическое зеркало радиуса 1, обращенное внутренней зеркальной поверхностью к плоскости, причем так, что ось симметрии зеркала перпендикулярна к плоскости Р в точке А. Зная, что наименьший угол между лучами, отраженными зеркалом и плоскостью Р, равен 15°, определить расстояние от зеркала до плоскости и радиус освещенного на плоскости Р круга.

Пусть наименьший угол между отраженными лучами и плоскостью Р равен α(рис.).

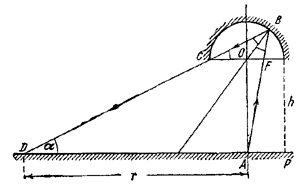
Такой угол образует луч, проходящий через край зеркала С после однократного отражения в точке В.

По условию задачи CF || DA; следовательно, ∠ОСВ =∠ОВС =α. Из условия отражения в точке В следует ∠OBF = α. Поэтому в треугольнике OBF имеем:

∠BOF = 2α, ∠OFB = 180^o— 2α — α = 180° — 3α.

Обозначим расстояние от зеркала до плоскости через h, а радиус освещенного круга AD через r. Так как радиус зеркала равен 1, то

(1)

Из треугольника OBF по теореме синусов находим:

В силу подобия треугольников CBF и DBA высоты в них пропорциональны сторонам, так что

или

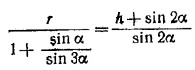
Решая уравнения (1) и (2) совместно, находим:

Подставив сюда данную в задаче величину α=15°, получим:

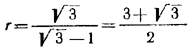
Далее,

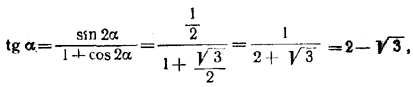
поэтому из (1) получим: