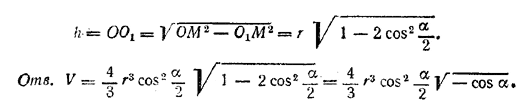Радиус шара, вписанного в четырехугольную правильную пирамиду, равен r. Двугранный угол, образованный двумя соседними боковыми гранями этой пирамиды, равен α. Определить объем пирамиды,.имеющей вершину в центре шара, а вершины основания — в четырех точках касания шара с боковыми гранями данной пирамиды.

Центр О вписанного шара (рис.) лежит на высоте пирамиды, а точки касания К, L, М, N шара с боковыми гранями лежат на апофемах ЕК₁, EL₁, EM₁, EN₁ (ср. задачу 266). Четырехугольник KLMN - квадрат, являющийся основанием пирамиды, объем которой требуется определить.

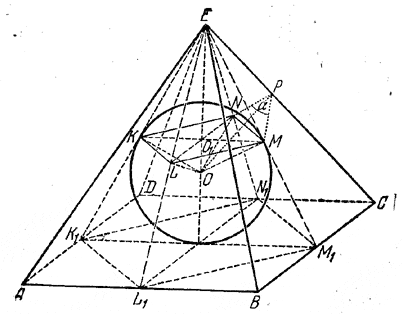
Проведем через радиусы ОМ и ON плоскость NOM. Она будет перпендикулярна к грани ВЕС (так как проходит через прямую ОМ, перпендикулярную к плоскости ВЕС), а также к грани DEC (так как проходит через ON). Следовательно, плоскость NOM перпендикулярна к ребру ЕС.

Пусть Р - точка пересечения плоскости NOM с ребром ЕС. Тогда угол NPM есть линейный угол двугранного угла α. В четырехугольнике OMPN два угла (при вершинах М и N) прямые. Следовательно, ∠ NОМ =180° - α . Значит,

Из треугольника ОО₁М, где О₁M = ^a/_√2 находим