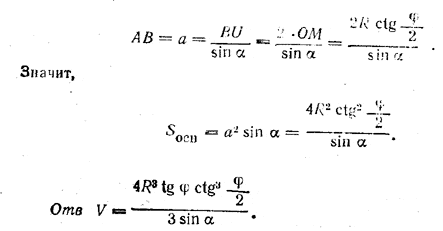Шар радиуса R вписан в пирамиду, в основании которой лежит ромб с острым углом α. Боковые грани пирамиды наклонены к плоскости основания под углом φ. Найти объем пирамиды.
Центр О1 шара, вписанного в пирамиду (если в эту пирамиду можно вписать шар), должен отстоять на равных расстояниях от боковой грани ВЕС и от основания ABCD (рис.).
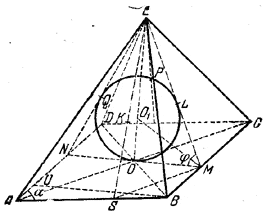
Поэтому он должен лежать на биссекторной плоскости двугранного угла φ при ребре ВС. Точно так же О1 лежит на биссекторных плоскостях двугранных углов φ при ребрах АВ, AD, DC. Значит, все боковые грани пирамиды O1ABCD (не изображенной на чертеже) наклонены к плоскости основания под одним и тем же углом φ/2
Следовательно, высота О1О пирамиды O1ABCD проходит через центр О окружности, вписанной в ромб ABCD (см. задачу 425). Через тот же центр проходит высота ЕО данной пирамиды. Значит, центр O1 шара лежит на высоте EO.
Точка касания шара с плоскостью грани, ВЕС есть основание L перпендикуляра, опущенного из центра О1 шара на плоскость ВЕС. Отсюда следует, что плоскость O1EL перпендикулярна к грани ВЕС (доказать!). Вместе с тем плоскость O1EL перпендикулярна к плоскости основания ABCD (так как проходит через высоту EO). Следовательно, плоскость O1EL перпендикулярна к ребру ВС. Значит, прямая MN, по которой пересекаются плоскости O1EL и ABCD, есть высота ромба (проведенная через его центр О). То же имеет место для остальных трех точек касания с боковыми гранями (K, Q и Р).
Отсюда вытекает следующее построение. Изображаем высоту NOM ромба ABCD (желательно, чтобы она была горизонтальной), строим сечение NEM (равнобедренный треугольник) и изображаем окружность, вписанную в треугольник NEM. Точки L и Q, в которых эта окружность коснется сторон ME н NE, будут точками касания шара с гранями ВЕС и AED. Чтобы изобразить точку К, проведем MS || АС. Тогда прямая OS (не показанная на чертеже) изображает другую высоту ромба (доказать!). Проводим прямую ES и через точку L проводим (не изображенную) прямую LK || MS. Четвертая точка Р строится аналогично. Из этого построения следует, что шар с центром О1 и радиусом R = O1L действительно вписан в пирамиду.
Решение. Из треугольника МОО1 находим
ОМ = OO1 ctg φ/2 = R ctg φ/2,
так что
Н = ОЕ = ОМ • tg φ = R ctg φ/2 tg φ.
Далее из треугольника BUA (где BU || МN) находим