Найти двугранный угол φ между основанием и боковой гранью правильной четырехугольной пирамиды, зная, что радиус описанного около пирамиды шара в 3 раза больше радиуса вписанного в нее шара.
Обозначим через r радиус вписанного шара, а через R радиус описанного шара.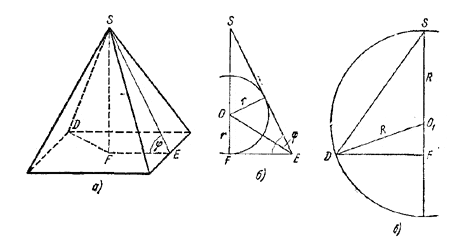
Рассмотрим сначала треугольник SFE, одна из сторон которого SF является высотой пирамиды, а другая SE - высотой боковой грани (рис. а). Пусть О - центр вписанного шара. Из треугольников SFE и OFE (рис. б) имеем:
FE = r ctg φ/2,
SF = r ctg φ/2tg φ.
Очевидно, далее, что
DF = EF√2
Обращаясь к рисунку в, где изображено сечение, проведенное через ось пирамиды и ее боковое ребро, мы легко найдем:
DO12 = O1F2 + DF2
или
R2 = (SF - R)2 + DF2.
Отсюда
![]()
Так как R = 3r, то, подставляя сюда найденные ранее выражения для SF и DF, получаем уравнение относительно φ:
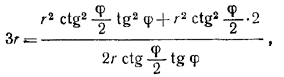
или после упрощения
6 tg φ/2tg φ = 2 + tg2φ.
Положим, далее, tg φ/2 = z. Заметив, что ![]() , мы приходим к уравнению
, мы приходим к уравнению
7z4-6z2 + 1 = 0.
Отсюда
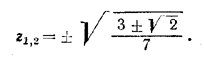
Так как z > 0, то возможны лишь два ответа:
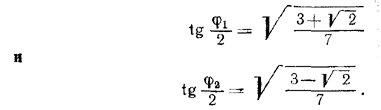
Похожие примеры: