В сферу радиуса R вписан правильный тетраэдр, и все его грани продолжены до пересечения со сферой. Линии пересечения граней тетраэдра со сферой вырезают из ее поверхности четыре сферических треугольника и несколько сферических двуугольников. Вычислить площадь каждого из этих двуугольников и треугольников

Всего получается 6 двуугольников (по числу ребер) и 4 треугольника.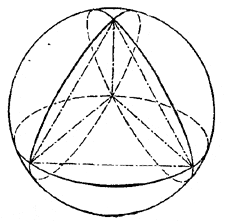

Обозначим через S₁ площадь каждого из треугольников и через S₂ - площадь каждого из двуугольников. Имеем:

4S₁ + 6S₂ = 4πR². (1)

Пусть S₀ - сумма площадей одного треугольника и трех прилежащих к нему двуугольников. S₀ есть площадь сферического сегмента, отсеченного плоскостью грани тетраэдра. Эта площадь равна 2πRh, где h - высота сегмента. Так как высота тетраэдра делится центром сферы в отношении 3:1 (см. задачу 249), то

H = R + ¹/₃R = ⁴/₃R

откуда находим h = 2R -⁴/₃R= ²/₃R.

Далее,

S₁+ 3S₂ = 2πR•²/₃R = ⁴/₃ πR². (2)

Решив систему, состоящую из уравнений (1) и (2), относительно неизвестных S₁ и S₂, получаем:

S₁ = ²/₃ πR², S₂ = ²/₉ πR²