Площадь S сегмента равна площади соответствующего сектора ОАВ минус площадь треугольника АОВ. Из геометрии известно, что площадь кругового сектора вычисляется по формуле: $$ S_1=\frac{1}{2}Rl $$

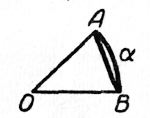
, где l - длина ограничивающей его дуги. Так как \(l = \alpha R\), то \(s_1 = \frac{1}{2}R^{2}\alpha \)

Площадь треугольника равна $$ s_2 = \frac{R^2 sin\alpha}{2} $$

Искомая площадь сегмента равна $$ S = s_1 - s_2 =\\= \frac{R^2 \alpha}{2} - \frac{R^2 sin\alpha}{2} =\\= \frac{R^2}{2}(\alpha - sin\alpha) $$