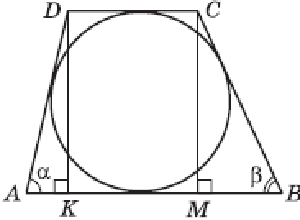
Пусть ABCD — данная трапеция, AB и CD — ее основания, DK и CM — перпендикуляры, опущенные из точек C и D на прямую AB. Искомое отношение не зависит от радиуса круга. Поэтому будем считать, что радиус равен 1. Тогда площадь круга равна ?, найдем площадь трапеции. Так как треугольник ADK прямоугольный, то

$$ AD=\frac{DK}{sin\alpha}=\frac{2}{sin\alpha} $$

Аналогично, из прямоугольного треугольника BCM находим, что \( BC=\frac{2}{sin\beta} \) Поскольку в данную трапецию можно вписать окружность, то суммы противоположных сторон равны:

AB + CD = AD + BC,

откуда находим:

$$ AB + CD = \frac{2}{sin\alpha}+\frac{2}{sin\beta}=\frac{2(sin\alpha + sin\beta)}{sin\alpha\cdot sin\beta} $$

Значит, площадь трапеции есть \(S=\frac{1}{2}(AB+CD)\cdot DK=\frac{2(sin\alpha + sin\beta)}{sin\alpha\cdot sin\beta}\)

и искомое отношение равно \( \frac{2(sin\alpha + sin\beta)}{\pi sin\alpha\cdot sin\beta} \)