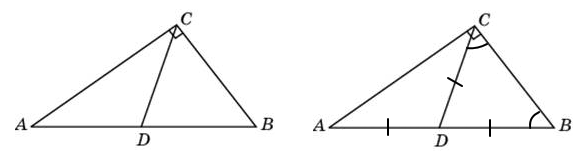
В треугольнике ABC CD - медиана, угол C равен 90°, угол B равен 24°. Найдите угол ACD. Ответ дайте в градусах.

Важное утверждение:

В прямоугольном треугольнике медиана равна половине гипотенузы.

(Так как угол С равен 90°, то, если бы мы описали вокруг треугольника окружность, дуга ACB опиралась бы на диаметр. То есть гипотенуза AB — диаметр описанной окружности. Центр описанной окружности лежал бы на середине гипотенузы, в точке D на рисунке. И DA=DС=DB=R.)

Итак, DC = AB/2 = DB. Значит, треугольник BDC — равнобедренный, и его углы при основании равны. То есть

$$ \angle DCB = \angle B = 24° \;\;\; \angle ACD = \angle C - \angle DCB = 90° - 24° = 66° $$