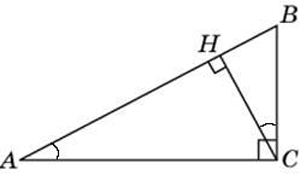
Начнем решение с доказательства равенства углов А и НСВ.

(Полезно знать и более общее утверждение: "Высота, проведенная из прямого угла прямоугольного треугольника делит его на два подобных треугольника, и оба эти треугольники подобны исходному." На рисунке угол A равен углу HCB, угол B равен углу HCA.)

Сумма острых углов в прямоугольном треугольнике равна 90°

Поэтому из \(\Delta\)AHC ∠A + ∠ACH = 90°

$$ \left. \begin{array}\angle A = 90° - \angle ACH\\ \angle HCB = \angle C - \angle ACH = 90° - \angle ACH\end{array}\right\}\\ \Rightarrow \angle HCB = \angle A \Rightarrow tg\angle HCB = tg\angle A = 5 $$

Из \( \Delta AHC \;\; tg\angle A = 5 = \frac{HC}{AH} \Rightarrow HC=5AH \)

Из \( \Delta CHB \;\; tg\angle HCB = 5 = \frac{HB}{HC} \Rightarrow HB=5HC=5\cdot(5AH)=25AH \)

Итак, HB = 25AH

$$ \left. \begin{array}AH+HB = AH+25AH=26AH\\ AH+HB = AB = 13\end{array}\right\} \Rightarrow 26AH=13; \;\; AH=\frac{13}{26}=0,5 $$

BH = AB - AH = 13 - 0,5 = 12,5