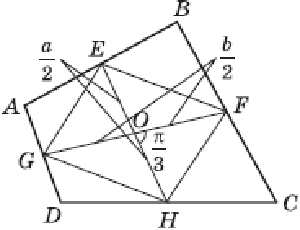
Известно, что если соединить последовательно середины сторон произвольного четырехугольника, то получится параллелограмм. В нашем случае EFHG — параллелограмм и O — точка пересечения его диагоналей. Тогда

$$ EO=OH=\frac{a}{2}, \;\; GO=OF=\frac{b}{2} $$

Применим к треугольнику FOH теорему косинусов:

$$ FH=\sqrt{OF^2 + OH^2 - 2OF\cdot OH\cdot cos\angle FOH} = \frac{\sqrt{a^2 + b^2 - ab}}{2} $$

Так как FH — средняя линия треугольника BCD, то \(BD=2FH=\sqrt{a^2 + b^2 - ab}\)

Аналогично, применив теорему косинусов к треугольнику EFO, получим, что

$$ EF=\frac{1}{2}\sqrt{a^2 + b^2 + ab} $$

откуда \(AC=2EF=\sqrt{a^2 + b^2 + ab}\)

Ответ: \(AC=\sqrt{a^2 + b^2 + ab}\), \(BD=\sqrt{a^2 + b^2 - ab}\)