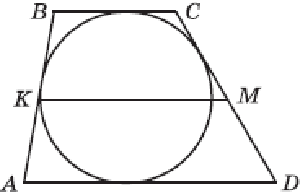
Пусть ABCD — данная трапеция, AB = 3 и CD = 5 — ее боковые стороны, точки K и M — середины сторон AB и CD соответственно. Пусть, для определенности, AD > BC, тогда площадь трапеции AKMD будет больше площади трапеции KBCM. Так как KM — средняя линия трапеции ABCD, то трапеции AKMD и KBCM имеют равные высоты. Поскольку площадь трапеции равна произведению полусуммы оснований на высоту, то верно следующее равенство:

$$ \frac{S_{AKMD}}{S_{KBCM}}=\frac{AD+KM}{KM+BC}=\frac{11}{5} $$

Далее, так как в трапецию ABCD можно вписать окружность, то AD + BC = AB + CD = 8. Тогда KM = 4 как средняя линия трапеции ABCD. Пусть BC = x, тогда AD = 8 – x. Имеем:

$$ \frac{S_{AKMD}}{S_{KBCM}}=\frac{12-x}{x+4}=\frac{11}{5} \Leftrightarrow x=1 $$

Значит, BC = 1 и AD = 7.

Ответ: 1 и 7.