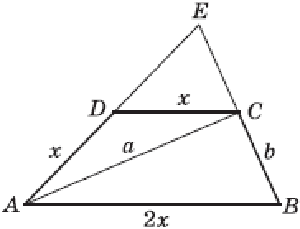
Пусть E — точка пересечения продолжений боковых сторон трапеции и CD = x, тогда AD = x, AB = 2x. Отрезок CD параллелен отрезку AB и вдвое его короче, значит, CD является средней линией треугольника ABE. Следовательно, CE = BC = b и DE = AD = x, откуда AE = 2x. Итак, треугольник ABE равнобедренный (AB = AE) и AC — его медиана. Поэтому AC является и высотой этого треугольника, и значит,

$$ S_{\Delta ABE}=\frac{1}{2}BE\cdot AC=ab $$

Так как треугольник DEC подобен треугольнику AEB с коэффициентом подобия \( k=\frac{1}{2}\), то

$$ S_{\Delta DEC}=\frac{1}{4}S_{\Delta AEB}=\frac{ab}{4} \Rightarrow S_{ABCD}=\frac{3ab}{4} $$ Ответ: \(\frac{3ab}{4}\)