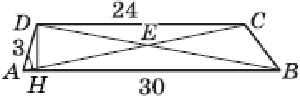
Пусть DH — высота трапеции. Из треугольника ADH находим, что \(DH=3sin60°=\frac{3\sqrt3}{2}\)

Так как высота треугольника ABC, опущенная из вершины C, равна высоте DH трапеции, имеем:

$$ S_{\Delta ABC}=\frac{1}{2}AB\cdot DH=\frac{45\sqrt3}{2} $$

Далее из подобия треугольников ABE и CDE получаем, что \(\frac{AE}{CE}=\frac{5}{4}\). Следовательно, \(\frac{EC}{AC}=\frac{4}{9}\)

$$ \frac{S_{\Delta BCE}}{S_{\Delta ABC}}=\frac{4}{9} \Rightarrow S_{\Delta BCE}=10\sqrt3 $$

Ответ: \(10\sqrt3\)